データを可視化!ボートレースの「分布」あるある3選
過ごしやすい季節になり、秋がやって来ましたね。
秋といえば文化祭の季節。陽の短くなった通学路を歩く学生さんを見かけると「文化祭の準備かな」と昔を思い出し、心が和みます。
とはいいつつ、私には学生時代のよい記憶があまりなかったりするのですが──

数字が苦手でも大丈夫、データ分析の第一歩
この記事を読んでくださっている方の大半はボートレースファンだと思っていますが、もしかすると「データ分析」という言葉に身構えてしまう方も多いかもしれません。
暗い部屋でパソコンに向かい、難しい数字を並べている──そんなイメージを持つ方もいるでしょう。
これは少し偏見ですが、実際に難しい分析をしている方もたくさんいます。
ただ、データ分析はそれだけではありません。実際、専門家でも必ず通ってきたテーマが今回の内容です。
それでは「分布」の話を始めましょう。

黒板に正の字──それが「分布」
「分布」という言葉を、皆さんも一度は聞いたことがあると思いますが、おおむねそのイメージで間違いありません。
今回、どのようなことを見ていただくかを分かりやすくお話しするなら、文化祭の出し物を決める光景です。
クラス全員で「文化祭でやりたいこと」を出し合い、それを黒板に「正」の字で数える──思い出す方も多いでしょう。
それをボートレースを例にして、グラフで見てみるのが今回の内容です。
難しそうなことでも、このようにグラフにすることで、見えてくることがたくさんあります。
それを実感していただけたらなと考えています。

毒島選手のスタートタイミングを分析
秋といえば、12月のグランプリに向けての賞金争いが大詰めですが、昨年(2024年)のグランプリを制した毒島誠選手のあるデータを分析してみましょう。
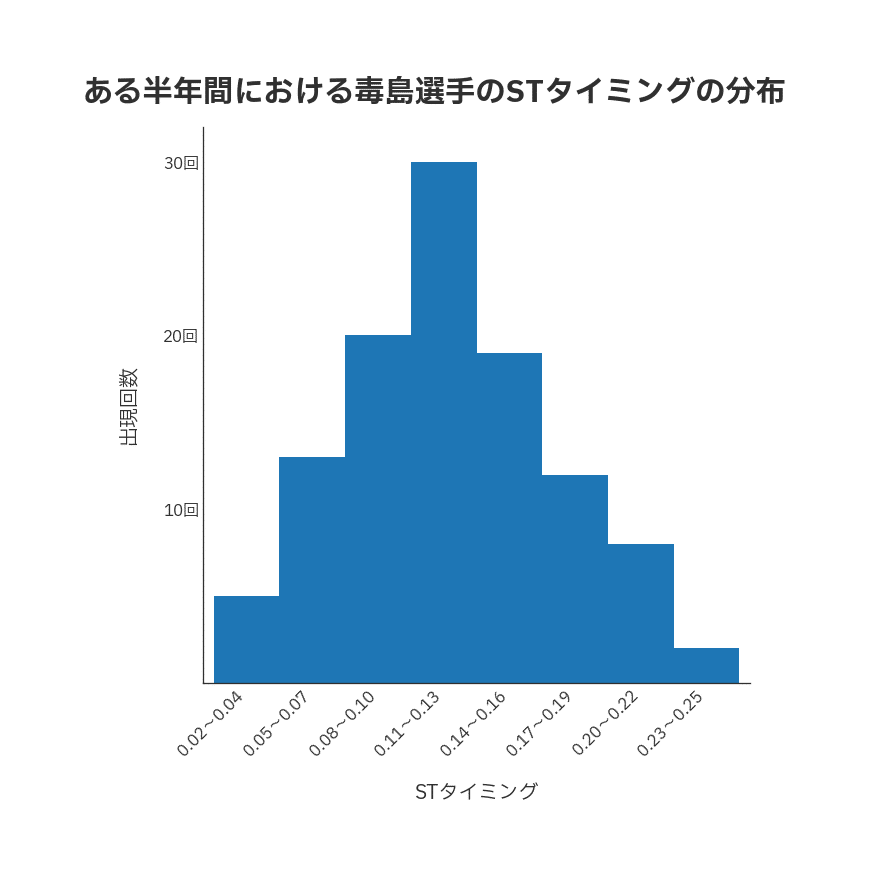
上のグラフは、ある半年間の毒島選手のスタートタイミングを示したもので、スタートタイミングが0.02から0.04だったレースが5回、0.05から0.07が13回──とカウントして作ったものです。
ちなみに、これは109レース分のデータから集計したもので、そこから計算したスタートタイミングの平均値は0.12でした。
グラフを見ると、平均値0.12付近を頂点に左右対称の山型になっています。
この形を詳しく見ていきましょう。
なお、一定のルールに基づき統計学で「参考外」とされた値は取り除いています。
統計学の基本「正規分布」とは
皆さんも毒島選手のレースを見ていて、このような形のグラフになることは想像できると思います。
何となく平均STタイミング付近が多く、それから離れるにつれて見る機会も徐々に減ってくる──そんなイメージでしょう。
そこで、上のグラフに線を書き加えます。
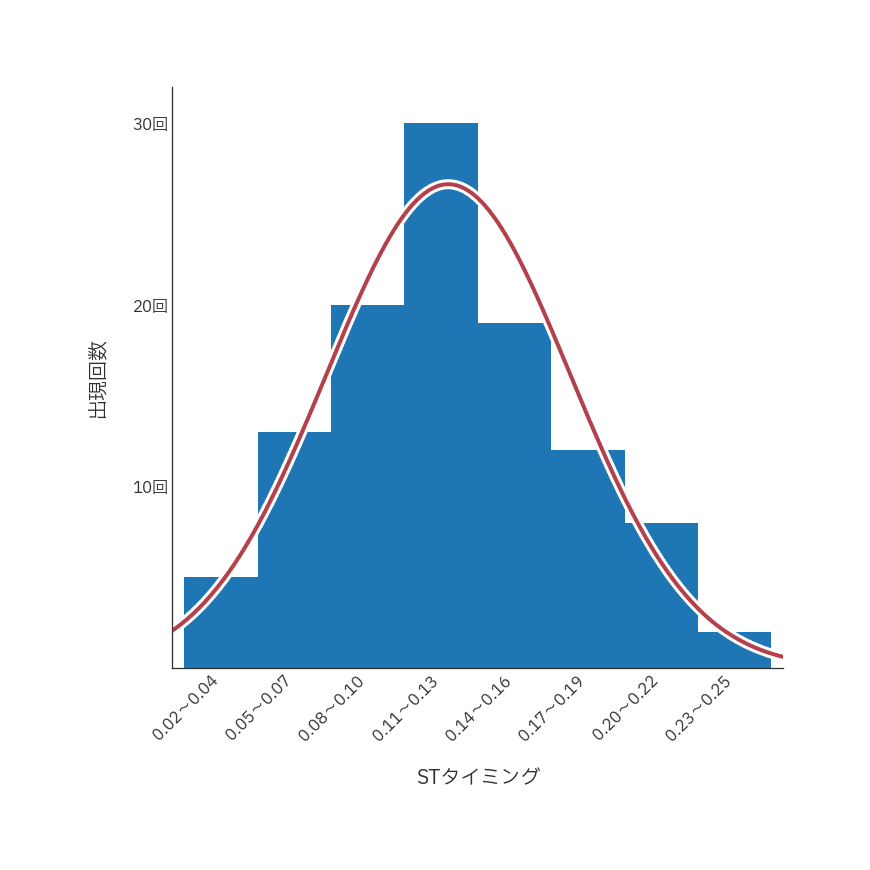
統計学に従って、きれいな山の形のような線を書き足してみました。
この赤色の線で書かれた形状には名前が付けられていて、「正規分布(せいきぶんぷ)」と呼ばれています。
つまり、毒島選手のスタートタイミングの分布は正規分布に近い形だということがグラフからわかります。
正確さより「似た形」と認識する大切さ
これは、毒島選手だけに限らず、ボートレーサーのスタートタイミングの分布をグラフにしてみると、正規分布に近似すると考えられます。
興味のある方は、ほかのレーサーのデータも調べてみるとおもしろいかもしれませんね。
ただ、お気付きの方もおられると思いますが、私は「近い形」や「近似」といった言葉で表現しています。
それは何も言い逃れをしているわけではなく、もし「ボートレーサーのスタートタイミングの分布が『正確な』正規分布なのか?」と聞かれると、同じような形状でも「No」と判断される場合が多いからです。
そして私は、似た形と認識するだけで十分だという考えを持っています。

統計学の礎「正規分布」のすごさ
ボートレースだけに限らず、日常生活の中にも正規分布やそれに近い事柄はたくさんあります。
とはいえ、それが完全な正規分布だといえるものはそう多くはない以上、そこに固執するのもどうかと考えています。
そして何より私がお伝えしたいのは、平均値付近が最も高い、左右対称の「山型」や「釣鐘型」と呼ばれるこの正規分布が統計学の礎(いしずえ)になっているということです。
これは、ただ集約しただけのデータから、予測や推測を可能にした偉大な分布だといえます。
ここでは「正規分布に似た分布が世の中に多くある」ということと、「正規分布のおかげで統計学を使ったいろいろな検証ができる」ということが伝われば、私は十分満足です。

払戻額に隠された分布の特徴
次に、このような分布をみてみましょう。ボートレースの払戻額です。
下はある半年間の3連単の払戻額の分布をグラフにしたものです。
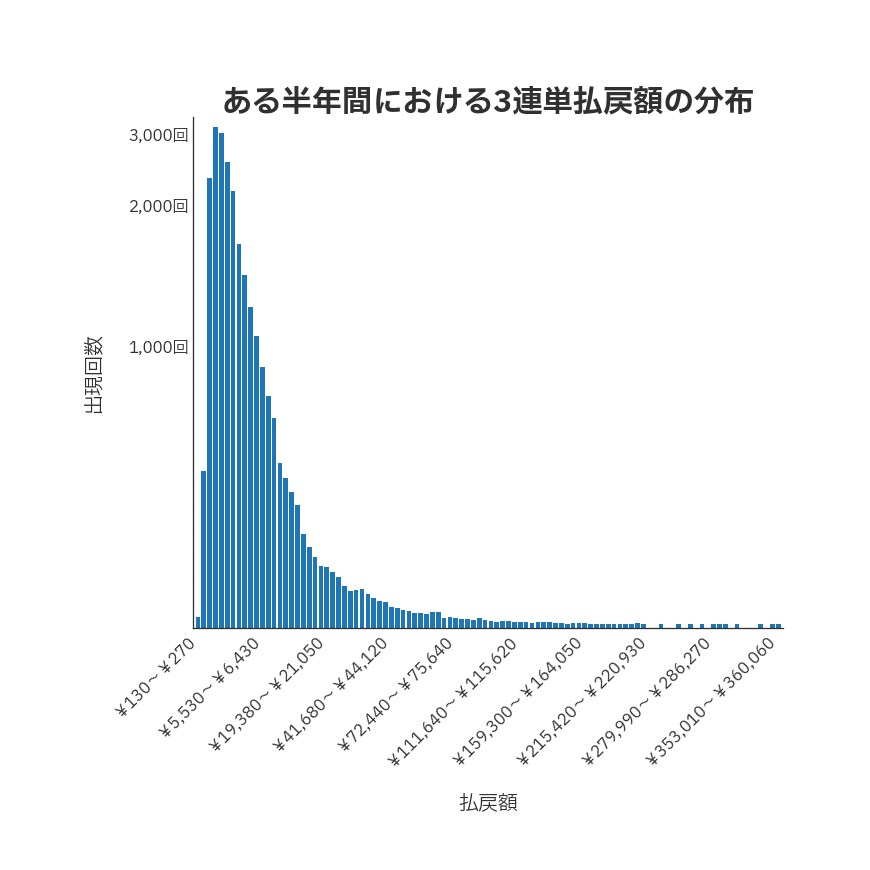
先ほどの正規分布がぎゅっと左に寄ったようなイメージで、右の裾が長くなっています。
このような分布は「対数正規分布(たいすうせいきぶんぷ)」と呼ばれ、身近な例でいえば年収の分布がこれに近い形状になるといわれています。
ただ、実はこのグラフは伝わりやすいように少し加工していて、正確に表すなら以下のようになります。

先ほど「右の裾が長い」と表現しましたが、これは大げさではなく、実際は想像以上に長いのです。
「裾の長い」分布が意味するもの
皆さんの中には、この分布が「対数『正規分布』」と呼ばれていることに違和感を持つ方もおられるかもしれません。
確かに正規分布に似た形状のものが左に寄っていることは確認できるとはいえ、正規分布と呼ぶにはほど遠いと感じてしまいます。
しかし、この分布にある魔法を掛けると不思議なことに正規分布に近似するのです。ただ、その魔法についてはここで触れません。

このように、ボートレースの払戻額の分布は対数正規分布に近似することが分かりましたが、ボートレースで勝ちにくい理由がこの分布にあると私は考えています。
いつかそのことも記事にしたいと考えています。ですので、この分布を頭の片隅に置いていただけると嬉しいです。

「今日は1号艇ばかり勝つ」現象の正体
次の分布を紹介する前に、少しイメージしてみてください。
日によって、「今日は妙に1アタマでの決着が多いな──」と感じるときがありませんか?
ボートレースはインコースが断然有利な競技なので、インを取ることが多い1号艇が1着になることが多いのも想像できます。
とはいえ、どう見てもレース結果の1着に1が多く並ぶ──そんなことがありますよね。
そこで、インコースの勝率が高いことで知られる、ボートレース徳山のある半年間における1日12レースのうち、1号艇が何回1着になったのかを日ごとにカウントしてみました。
その分布が下のようになります。
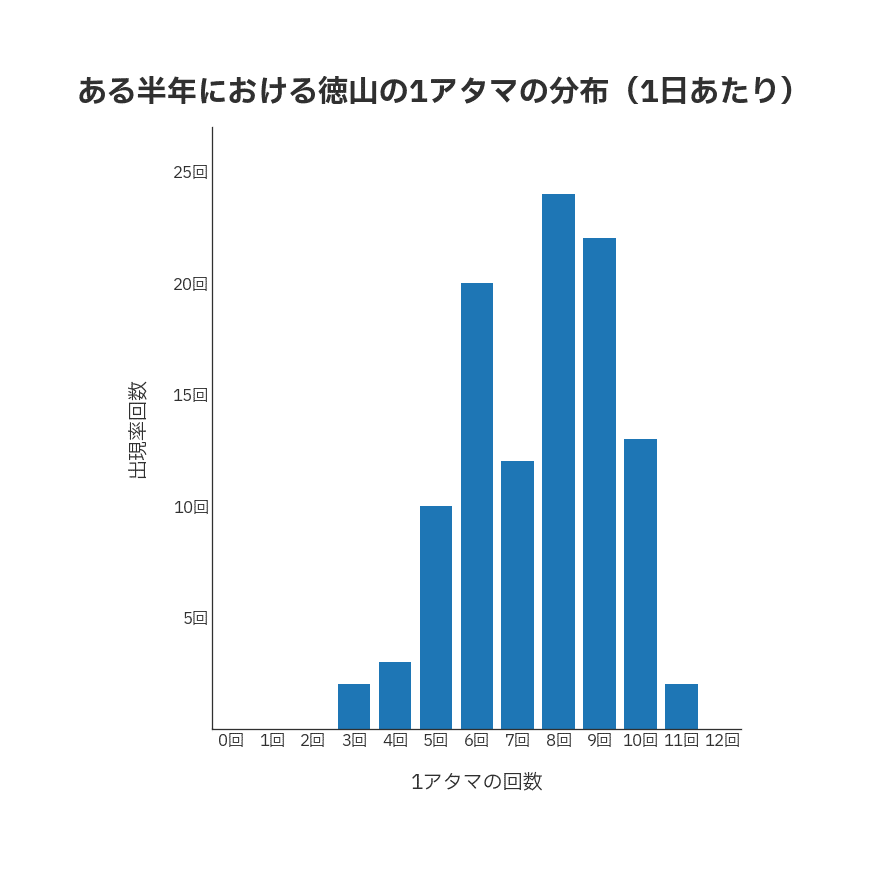
「カウント」とは何をしているのか?
少しだけ小難しい話をすると、ここでの「カウント」という作業は、下のようになります。
例えば、○月×日に徳山で1号艇が8回勝ったなら、「0回でしたか?」「1回でしたか?」と順に質問し、「8回でしたか?」で初めて1を加える、という仕組みです。
つまり、0回から12回までの13通りを「はい・いいえ」で確かめているのと同じです。
この話を覚えておいていただいて、上のグラフをこのように加工します。
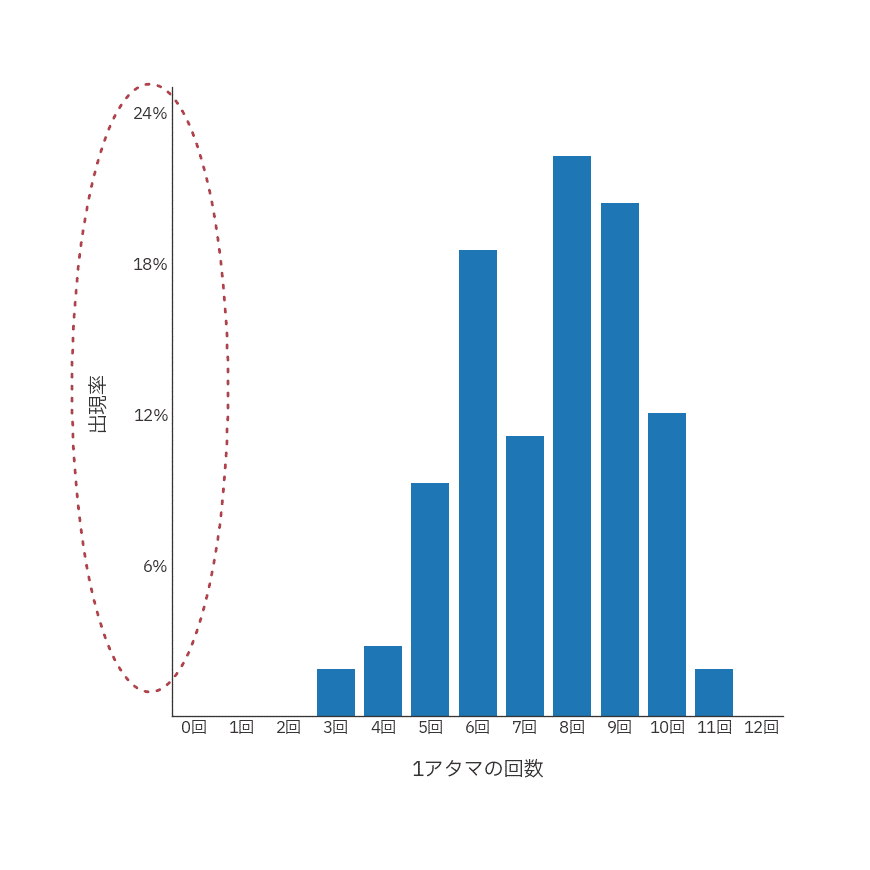
グラフの形は変わっていませんが、縦軸を「出現回数」から、その値を集計した数で割り算した「出現率」にしてみました。

的中率を分布で考えるとこうなる
上のような「はい・いいえ」などのふたつのうちのひとつに属する事柄の分布を「二項分布(にこうぶんぷ)」と呼びます。
これを身近な例でお話しするなら、的中と不的中の繰り返しを確率で表す「的中率」もそれに該当します。
例えば的中率25%の人は、日によって波はあるものの多くは25%前後に収まり、似たような分布になることが想像できます。
上のグラフは少し歪(いびつ)ではありますが、どこかで見た形状と似ていると感じた方もおられるかもしれません。
そうです。お察しの通り、二項分布はデータ量が十分であれば正規分布に近似するとされています。

可視化すればデータはもっと語り出す
今回は、ボートレースで見かけるデータ分布を3つ紹介しました。
データ分析では、つい数字に頼りすぎて可視化を忘れがちです。
ただ、データの可視化は基本であり、この習慣がデータに対する想像力を養うと考えています。
皆さんも気になったデータがあれば可視化してみてください。きっと今見ている以上のものが見えてきますよ。