【第11回】 それでも江戸川は当地成績が重要なのか ［ボートレース×統計学］
前回の「ボートレース×統計学」では、全国勝率より当地勝率の高いレーサーが、全体とどれほど違いがあるのかを調べました。
その結果、当地に強いレーサーが特別多く、その節を勝っている訳ではないと分かりました。
ただし、集計期間や検証方法に左右されるため、この結果だけで当地成績を軽視すべきではありません。
とはいえ、せっかくこの定義で検証しているのですから、もう一歩踏み込み、面白い発見を探してみましょう。
あの場はなぜ特別視されるのか
これはあくまで私の印象ですが、24ある全ボートレース場の中には、「特に当地成績が重要」とされているところがあります。
それは、全場で唯一、河川を利用したボートレース場、ボートレース江戸川──
ボートレースファンからは「もはや別競技」と揶揄されることもありますが、実は私の大好きなボートレース場です。
そんなボートレース江戸川を攻略しようとすると、必ずこの情報に行き着きます。
そこで、今回の定義にもとづき、ボートレース江戸川で当地成績がどれほど重要なのかを調べてみましょう。
まとめると「ボートレース江戸川は、当地に強いレーサーの勝率は全体と比較して違いがあるのか？」という検証を行います。
勝率17.0%の成り立ちを考える
少しイメージを膨らませてみましょう。
前回の検証で、全ボートレース場の「当地に強い」レーサーの勝率は17.0%だということが確認できました。
ここで、「17.0%」という確率の成り立ちを考えます。
一般的に考えると、各ボートレース場の勝率には多少の差があるものの、概ねこの数値に近く、それをまとめた値が17.0%と考えるのが自然でしょう。
しかし、江戸川が「当地成績が重要」とされる以上、他場の勝率が数%程度でも、江戸川だけが群を抜いて高く、その結果が17.0%という値になっている可能性もなくはありません。
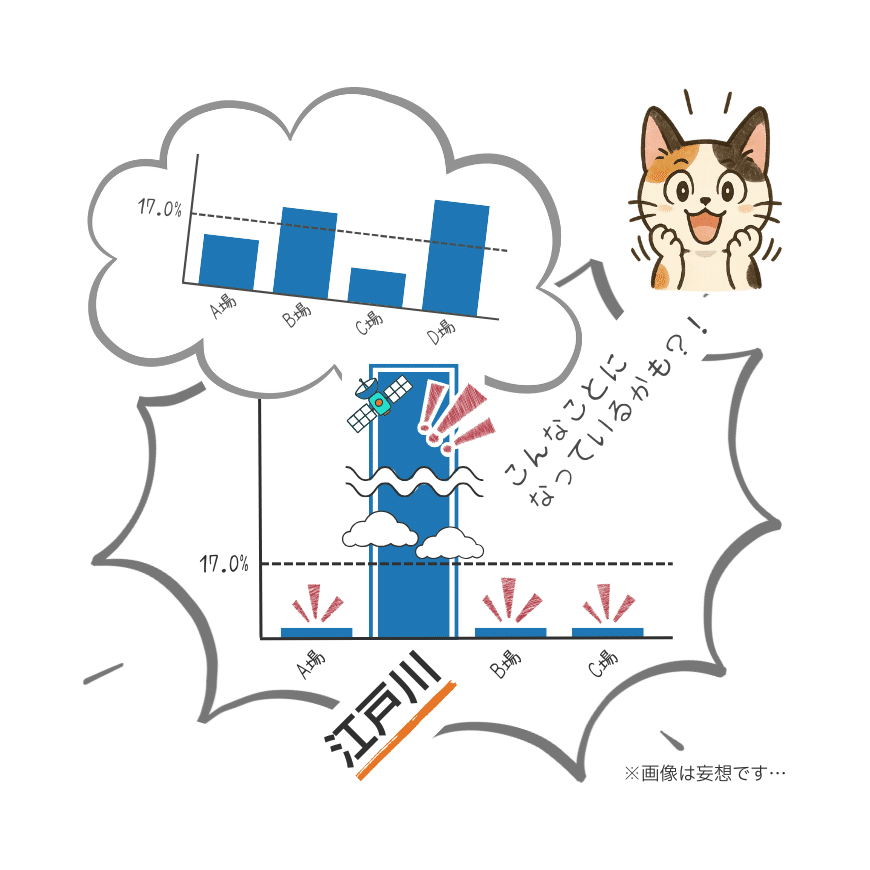
検定に必要なデータを整理する
まずは、「基準の確率」を確認しておきましょう。
前回と同じ半年間のデータから、今回は江戸川のレースデータのみを抽出し、そのレース数は474であることが分かりました。
すると、出走した全レーサーの数は2,844人（レース数 × 6選手）となり、そのうち1着を取ったレーサーは、レース数と同じく474人です。
つまり、474 ÷ 2844 の計算から得られる基準の確率は16.7%となります。
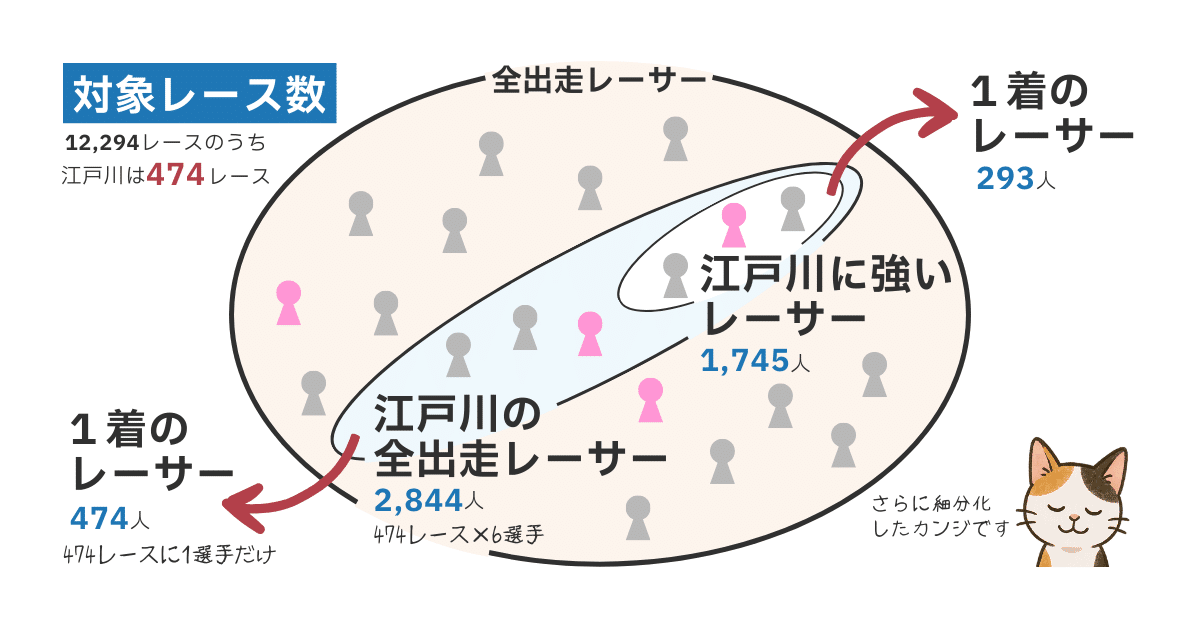
次に、「調べた確率」と「調べた数」にも触れておきます。
この期間に、江戸川で出走した2,844人のうち、全国勝率より当地勝率の方が高い「江戸川に強い」レーサーが1,745人でした。これが「調べた数」にあたります。
そして、そのレーサーが1着を取った確率は16.8%で、これが「調べた確率」です。
これで、母比率の検定における検定統計量を算出するための値、「基準の確率」「調べた確率」「調べた数」がすべて出揃いました。
では、下の図を参考に仮説検定を進めましょう。
検定前に決めておくルールの設定
上の流れに従って、事前に準備が必要な項目をここで設定しておきましょう。青色、緑色の項目です。
使用する統計学の手法は、上でもお話ししたとおり「母比率の検定」になります。
これは「江戸川の全出走レーサー」に含まれる「江戸川に強いレーサー」の勝率を調べるために、この手法を用います。
そして、「違いを知りたい」という目的から、それを確認できるルールを採用しましょう。
つまり、今回も母比率の検定（両側）で一応の結論を出します。
次に、「偶然と必然の境界線」を表す有意水準は、もっとも一般的な値で、私の記事でも採用するとしている5%という値とします。
検定の肝となる仮説の設定
そして、黄色の項目「仮説を立てる」へと進みます。
この統計学の手法は名の通り、仮説を検定するもの。そこで必要な、実際に検証する仮説「帰無仮説」と、これを否定（棄却）した場合に採用する「対立仮説」を設定しましょう。
まず、対立仮説は一般的には私たちが知りたいことを設定するとされています。
今回だと「江戸川に強いレーサーの勝率と、江戸川に出走した全レーサーの勝率には違いがあるといえる」とします。
そうなると、帰無仮説は「江戸川に強いレーサーの勝率と、全レーサーの勝率には違いがあるとはいえない」です。
このあと、帰無仮説を前提に検定統計量を算出し、その値で判断することになります。
検定統計量を算出して検証スタート
それでは、整理したデータを使って検定に必要な値を計算し、江戸川の全体勝率と「江戸川に強い」レーサーの勝率に違いがあるかを、統計学で一応の結論を出したいと思います。
少し詳しくいうと、「基準の確率」「調べた確率」「調べた数」から値を算出し、それを判定用のグラフに当てはめて判別します。
その位置によって帰無仮説を採用し「違いがない」とするのか、あるいは帰無仮説を棄却して対立仮説を採用し「違いがある」とするのか──と展開します。
それでは、母比率の検定の流れを追いかけてみましょう。
ここで算出される検定統計量
では、検定統計量を計算してみましょう。
計算式は次のようになっていて、それぞれの値を代入することで求めることができます。
なお、先ほど集計したボートレース江戸川の詳細データはこちらです。
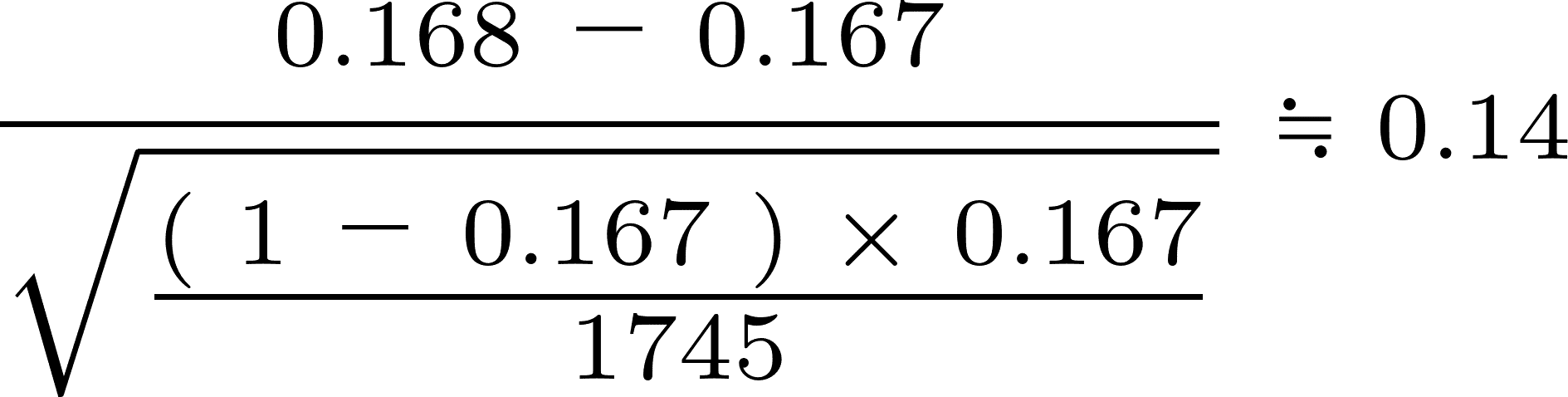
上のように、検定統計量は0.14と算出することができました。
この値をグラフの横軸に置き、棄却限界値を境に塗り分けられたどの部分に位置するかを確認しましょう。
なお、白色の部分なら帰無仮説を採用し、ピンク色（棄却域）にあれば棄却して対立仮説を採用します。
検定結果から見える江戸川の実態
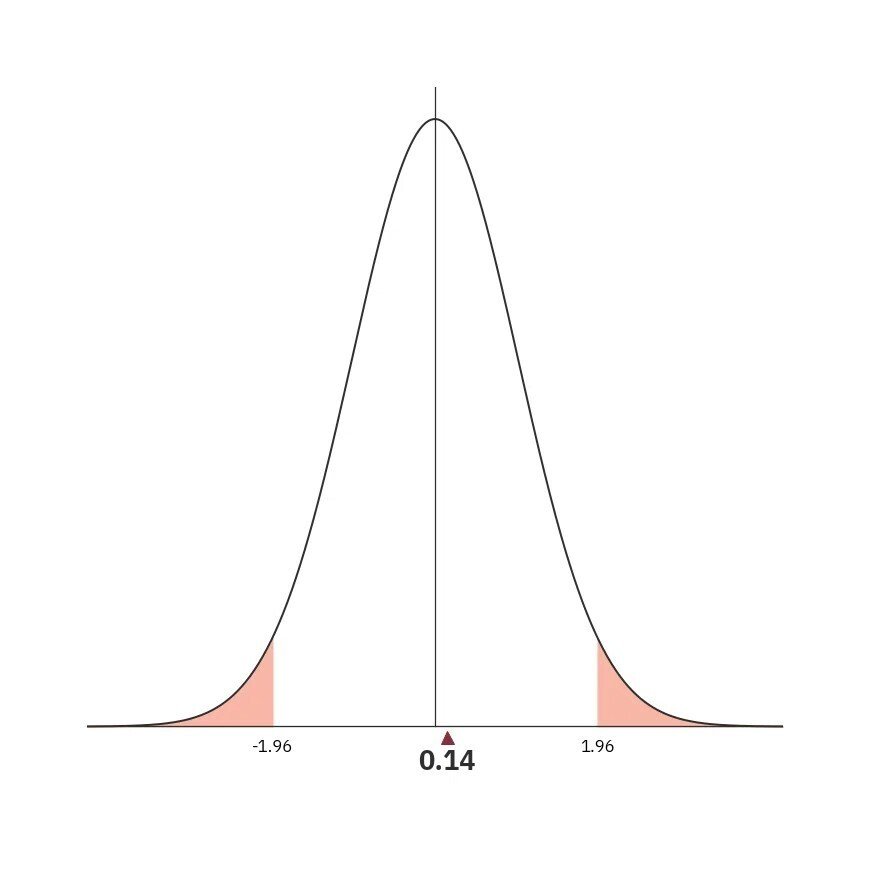
検定統計量は白色の部分にあります。
これは帰無仮説を棄却できない、つまり「江戸川に強いレーサーの勝率と、江戸川に出走した全レーサーの勝率には違いがあるとはいえない」と統計学が判断しました。
江戸川に強いレーサーの勝率は16.8%、全体は16.7%と違いはごくわずかで、統計学を用いても「違いがある」と判断するのは難しかったのです。
今回の検証をまとめると「ボートレース江戸川は、全体と比較して当地に強いレーサーの勝率が特別高いわけではない」となります。
この結果を踏まえると「江戸川は当地成績が特に重要」という格言を、どこまで信じてよいのか疑問に感じた方も多いでしょう。
私自身も同じように感じています──
次回、江戸川追求はまだ続く
残念ながら、今回のような定義ではボートレース江戸川の当地成績の重要性を引き出すことはできませんでした。
「全国勝率より当地勝率の方が高い」というシンプルな考え方ではなく、別の定義でデータを分析する必要がありそうです。
もし、当地成績のデータを活用するアイデアをお持ちの方がおられましたら、ぜひお話を聞かせてください。
──と、ここで検証を終えようとしたのですが、私はふと考えました。
「『当地成績が重要』とは、必ずしも1着だけを指すのではないのでは──」
次回、再度このシンプルな定義のもと、ボートレース江戸川のデータをさらに深く追求してみたいと思います。
最後まで読んでいただき、ありがとうございました。