【第12回】 続・それでも江戸川は当地成績が重要なのか ［ボートレース×統計学］
前回の「ボートレース×統計学」では、「当地成績が特に重要だ」とされるボートレース江戸川の出走レーサーについて、深掘りしました。
そこでは、全国勝率より当地勝率が高いレーサーを「江戸川に強い」と定義して検証した結果、江戸川に強いレーサーの勝率は、全体と比べても高いとはいえないことが分かりました。
ただ、「当地成績が重要」とは、1着だけを指すものではないのではないか──そう提案して、前回を締めています。
そこで、今回はボートレースの出走表にある「3連率」に注目して、江戸川における当地成績の重要性を解明していきます。
前回の結論を踏まえた新たな視点
3連率の検証を始める前に、おさらいを兼ねて、次のような話題から始めましょう。
前回はボートレース江戸川に焦点を当て、当地成績を検証しましたが、このような関心を持った方もおられるかもしれません。
他場の「当地に強い」レーサーは、どのような成績なんだろう──そこで、全24場の「当地に強い」レーサーの勝率がどうだったのかを調べてみました。
具体的には、従来の定義通り、全国勝率より当地成績が高いレーサーを「当地に強い」とし、各場ごとに勝率を全体と比較し、表にまとめました。
いつも難しい話にお付き合いいただいているので、この記事の前半くらいはラフに進めたいと思っています。
では、一覧をご覧ください。
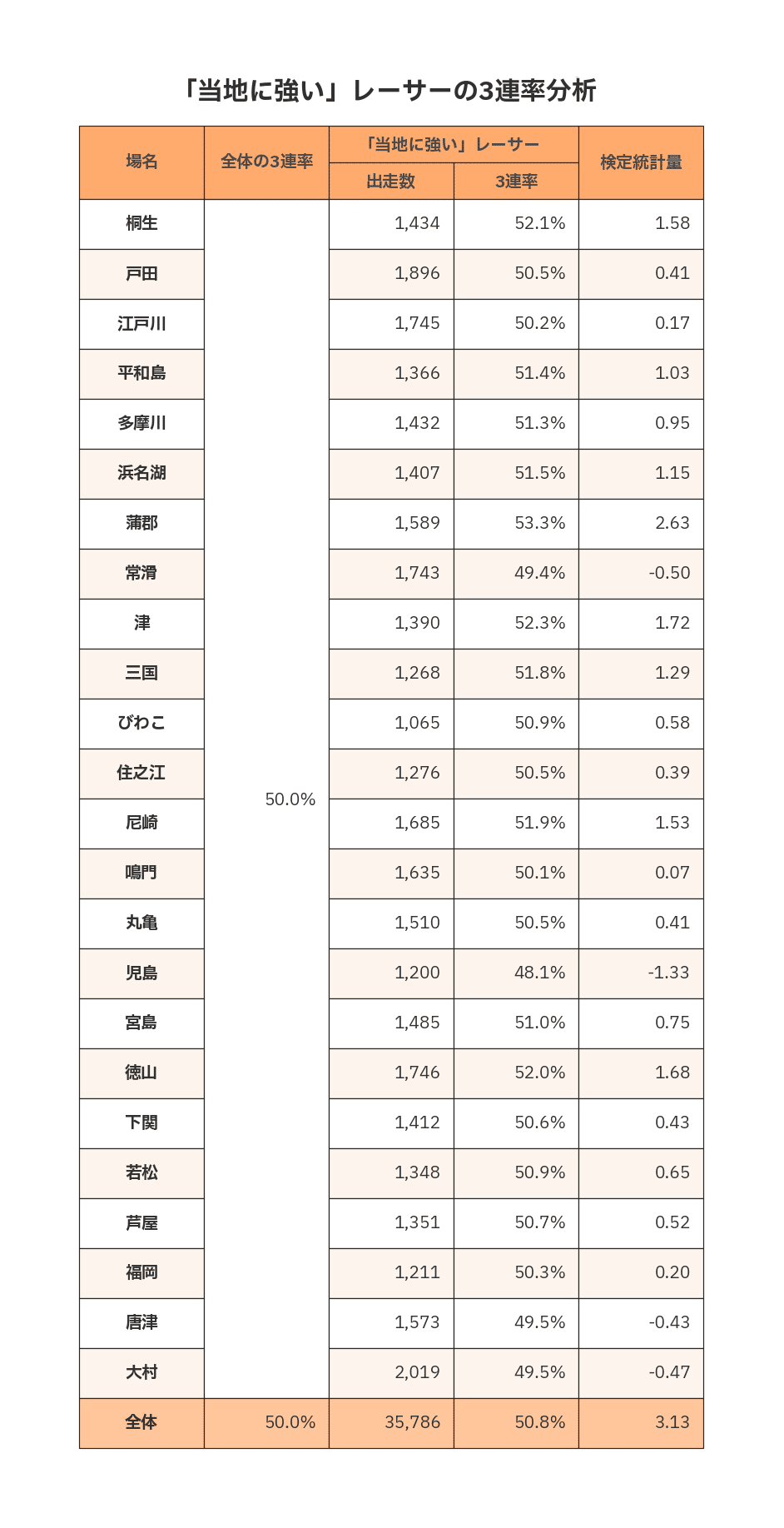
他場の「当地に強い」レーサー成績は？
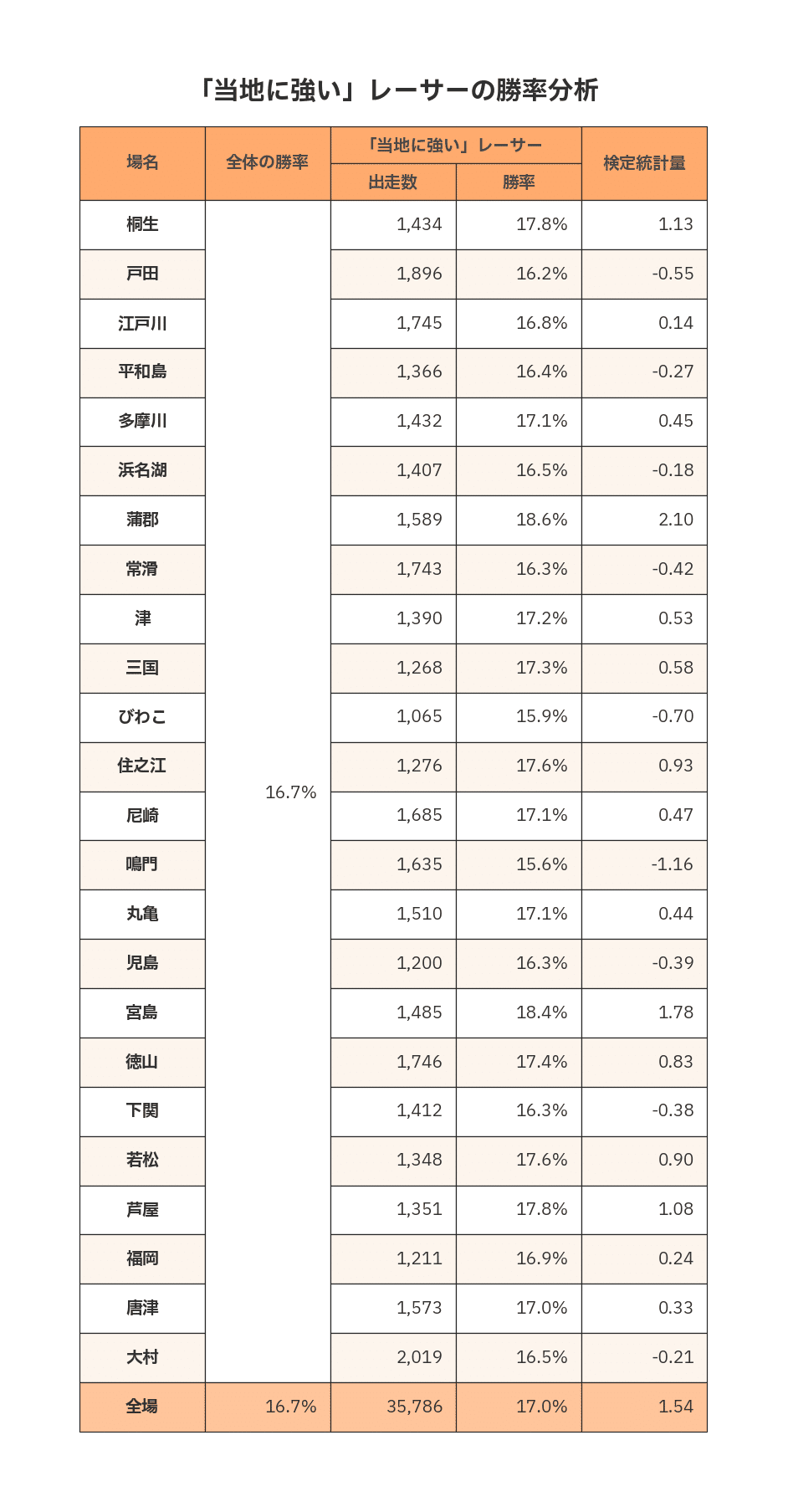
上の表には、全体の勝率と、各場における「当地に強い」レーサーの勝率、その出走数や、全体の勝率から算出した検定統計量を載せています。
勝率はおおむね15%台から18%台に分布しており、ボートレース場ごとの違いが見受けられます。
そこで、各場の統計検定量をひとつのグラフ上に並べ、位置関係を見てみましょう。
前回検証したボートレース江戸川との位置の違いに、注目してみてください。
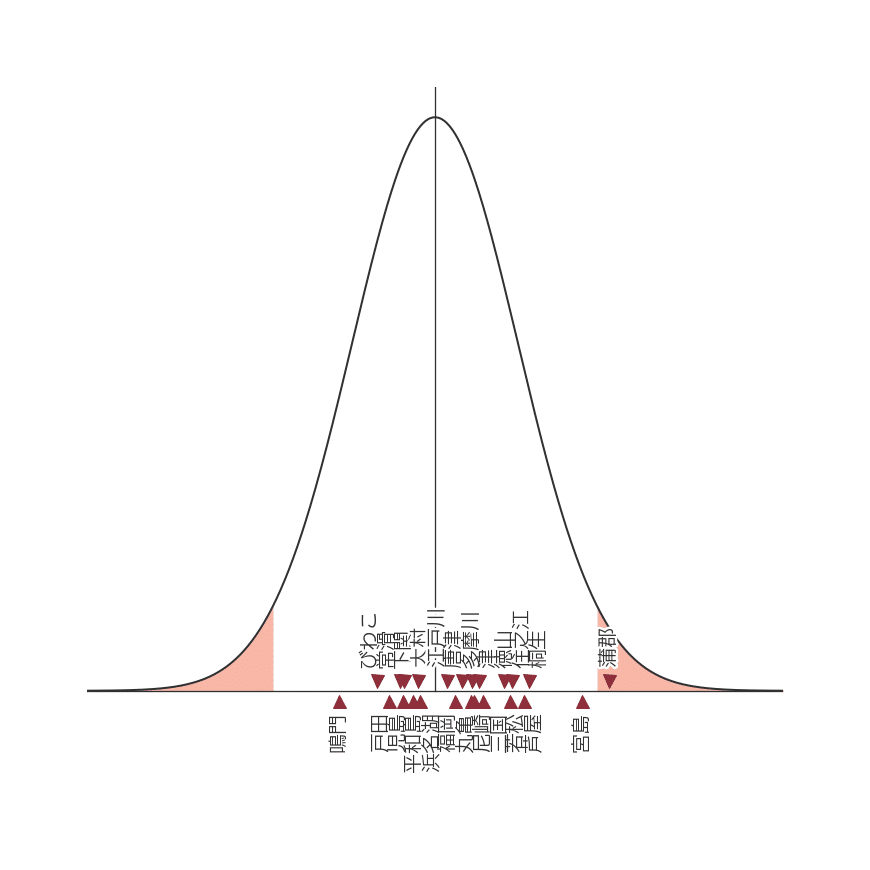
グラフを見ると、特にボートレース蒲郡の値が突出して高く、今回の定義で半年間集計した限りでは、蒲郡に強いレーサーの勝率は、全体の勝率16.7%と比べると違いがあると考えられます。
検定統計量で見える意外な位置関係
前回検証した江戸川との位置関係を比べると、それ以上に特徴的なボートレース場があることが見えてきます。
これらを踏まえると、当地に強いレーサーの勝率に関しては、江戸川は当地勝率の面で、平均的なボートレース場と位置付けられそうです。
このように、検定統計量を並べることで、ボートレース場同士の位置関係が分かり、意外な場も浮かび上がりました。
皆さんの好きなボートレース場は、どのような位置にあったでしょうか──もしよければ、お聞かせください。
それでは今回の本題、3連率から見る「『新・江戸川に強い』レーサーは3着以内によく入るのか」を検証してみましょう。
「新・江戸川に強い」を探して
先ほどからお話ししている通り、勝率の側面からみると、ボートレース江戸川は特徴のある場とはいえませんでした。
これを「3連率」という視点から見てみると、それはどう変わるのでしょうか。
1着に関しては平均的な値でしたが、2着や3着は「当地に強い」レーサーが極端に多く入り、3連率を大きく上げている可能性もなくはありません。
そうなると、当地に強いレーサーを軽視できない、つまり「江戸川は当地成績が重要」という定説は正しいと、結論付けることもできます。
それでは、同じ半年間の「新・江戸川に強い」レーサーのデータを抽出し、仮説検定で違いがあるかを検証します。
対象データから数字の土台を確認
まずは、検証に必要な「基準の確率」「調べた数」「調べた確率」の整理をしておきましょう。
今回対象となるのも、ある半年間にボートレース江戸川で行われた474レースです。
これは、全国3連率や当地3連率に「0.00」を含むレーサーを除いた、6艇でスタートして6艇がゴールしたレース数になります。
そして、レースに出走した全レーサーは 474×6艇 の2,844人で、3着以内に入ったレーサーは1,422人でした。
つまり、全体の3連率は 1422÷2844 の50.0%となり、これが「基準の確率」になります。
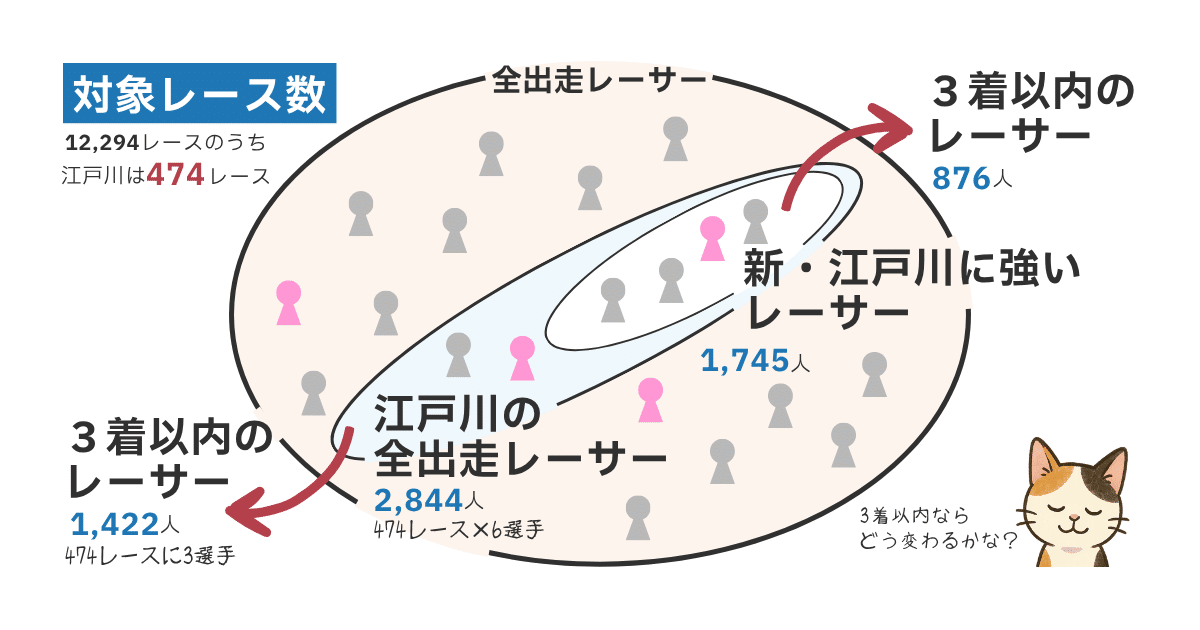
その全レーサーのうち、全国3連率より当地3連率の方が高かったレーサーは1,745人で、これが「調べた数」になります。
さらに調べると、そのうち3着以内に入ったのは876人だったので、「調べた確率」は 876÷1745 となり、50.2%と算出されました。
これで仮説検定に必要な値が出揃いました。早速、検証を進めましょう。
今回はテンポを少し速めますので、どうかお付き合いください。
仮説検定の前に整理すべきこと
それでは、上の仮説検定の流れに従って検証を進めましょう。ここでは、青色、緑色、黄色を一気に進めます。
今回の検証も、全体の3連率（比率）と江戸川3連率について調べるので、仮説検定の手法のひとつ、母比率の検定を選びます。
さらに、違いがあるのかを確かめたいので、その判断基準となる両側検定を採用しましょう。
つまり、この検証で使用する統計学の手法は「母比率の検定（両側）」となります。
そして、偶然と必然の境界線の基準となる有意水準は、もっとも一般的な5%とし、仮説の設定に進みます。
今回の検証で私たちが知りたいことは、「江戸川に強いレーサーの3連率は全体の3連率と比較して違いがあるのか」ということなので、対立仮説は「江戸川に強いレーサーの3連率と、全体の3連率とは違いがあるといえる」とします。
そうなると、帰無仮説は「江戸川に強いレーサーの3連率と、全体の3連率に違いがあるとはいえない」となり、これが実際に検証の対象となる仮説です。
このあと、帰無仮説を前提とした検定統計量を算出し、その値をグラフに配置して、帰無仮説を主張するか、棄却して対立仮説を採用するかを判断します。
統計が示したボートレース江戸川の姿
これで母比率の検定（両側）の準備がすべて整いました。仮説検定の流れに従って、上の赤色とオレンジ色の項目へと進みます。
先ほどデータをまとめた通り、検定統計量を算出するための値は以下のようになっています。
これを上の方程式に当てはめて算出し、グラフで判断するまでを一気に見てみましょう。
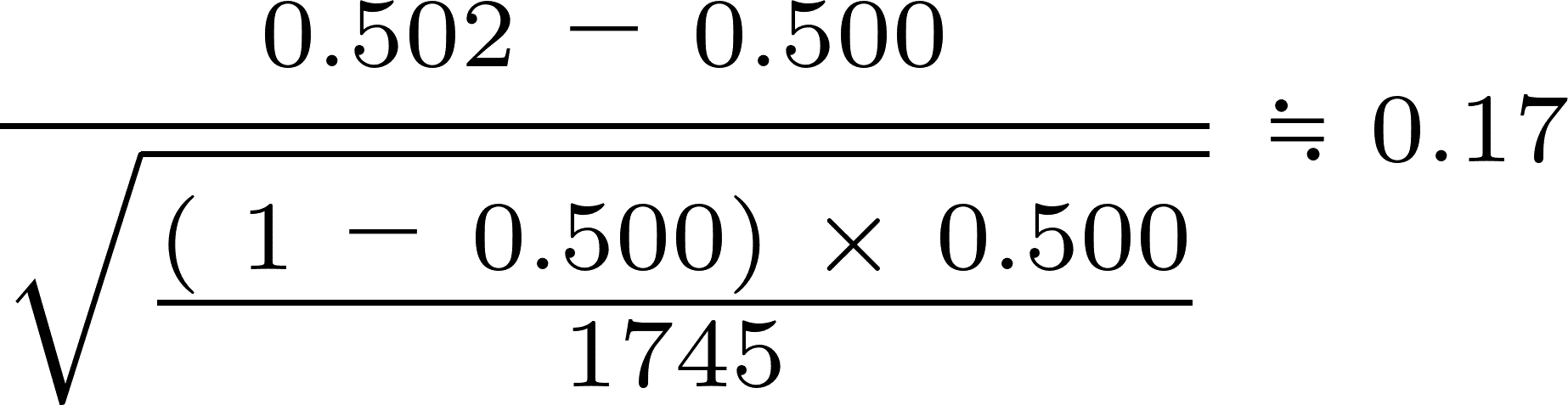
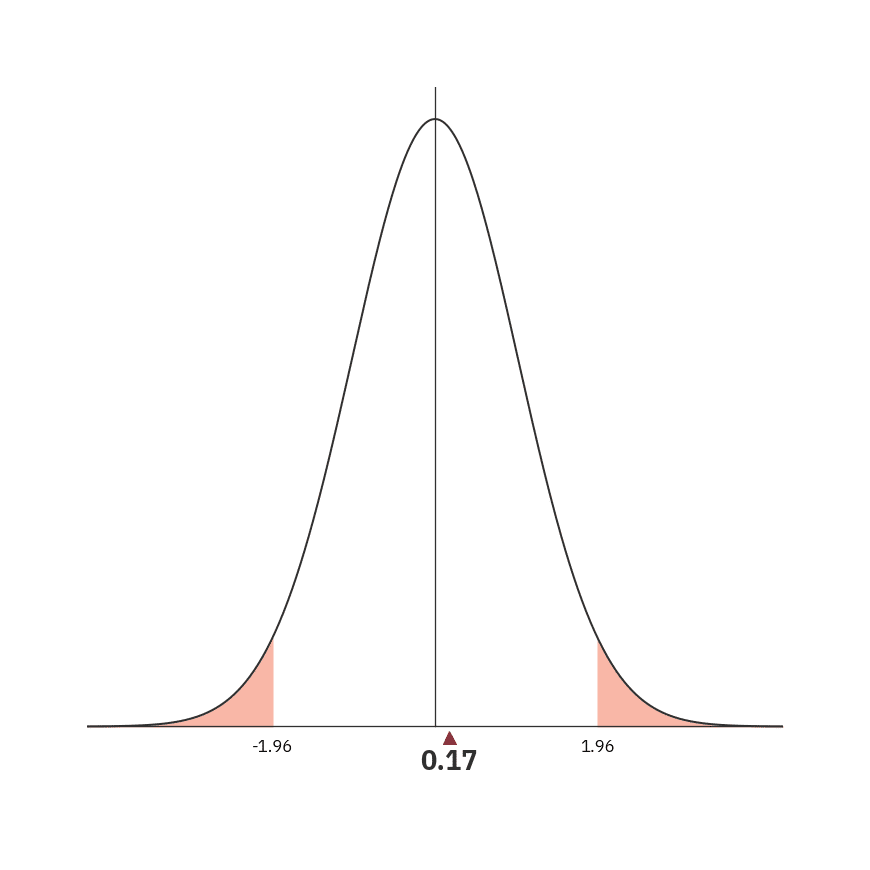
算出された検定統計量0.17は、グラフの白色の箇所にあり、棄却域（ピンク色）にはありません。
よって、帰無仮説を棄却できず、「江戸川に強いレーサーの3連率と、全体の3連率には違いがあるとはいえない」という主張を、統計学がしたことになります。
これを言い換えるなら、「『新・江戸川に強い』レーサーは、当地で特に多く3着以内に入っているわけではない」となります。
3連率からも有意差は見られず
今回も勝率の検証と同じく、「江戸川では当地成績が重要である」とはいえませんでした。
もちろん、「全国3連率より当地3連率の方が高い」という、シンプル過ぎる定義がいけなかったかもしれませんし、期間やデータ量で、結果も変わってくることも考えられます。
ただ、このように統計学を駆使することで、疑問に対して一応の結論を出せるのが、仮説検定をボートレースのデータ分析に活用する意味だと、私は思っています。
では最後に、この検証を全24場でおこなうとどうだったのか、その一覧と位置関係をご覧いただきましょう。
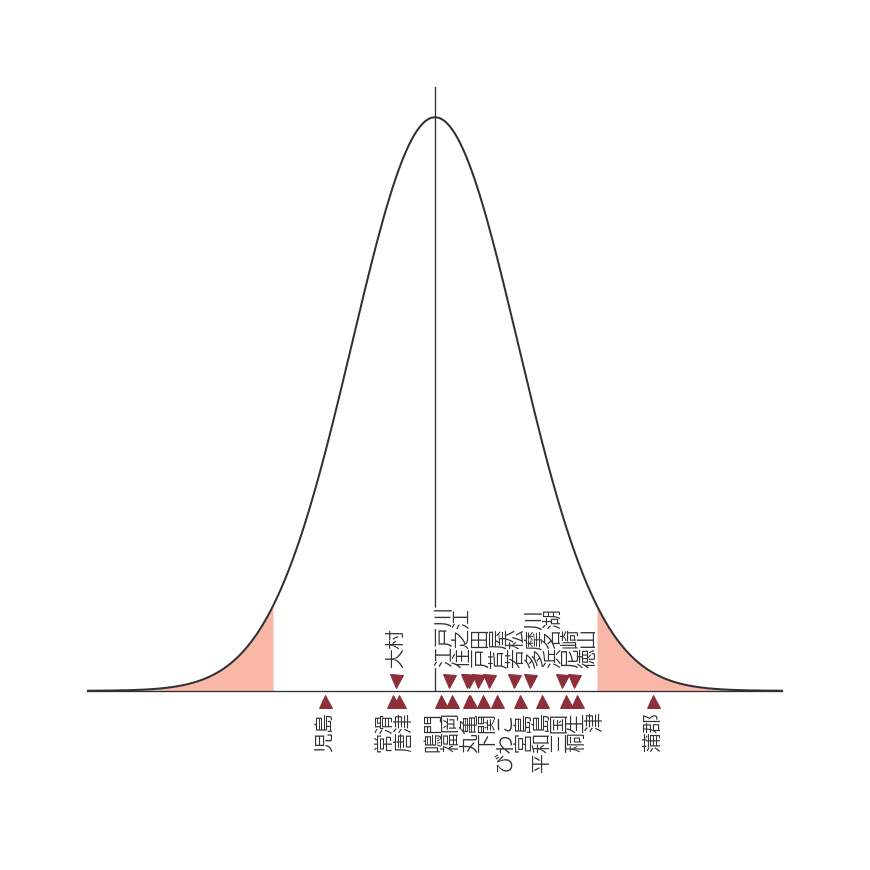
3連率で見た24場の位置関係
位置関係を見ると、やはりボートレース蒲郡は3連率でも突出した値になっていて、レース予想の際、ここに注目すると、良い結果につながる可能性も十分にあります。
今回で3回に渡ってお届けした当地成績についての検証は、一旦終わりますが、少し統計学に慣れてきた方なら、気付いたことがあるかもしれません。
ここでは詳しく触れませんが、ヒントは先ほどの一覧の最下部、「全体」の欄に隠されています──
今回も最後まで読んでいただき、ありがとうございました。
