【第10回】 「当地に強い」レーサーは本当に強いのか？ ［ボートレース×統計学］
前々回、前回と「ボートレースはスタートが揃うと何が起こるのか」をテーマにお届けしました。
この検証から、1コースは明らかに勝率が高くなること、ボートレース場ごとにスタートの揃いやすさに特徴があること、そして外のコースの飛躍が特に目立つことが分かりました。
一見、判断の難しい事柄も、数字で一応の結論を出せる点が、統計学をボートレースに取り入れる魅力だと感じています。
さて、今回は出走表にある「当地勝率」を舟券予想にどう盛り込むべきかを、統計学で検証します。
全国勝率と当地勝率の比較から見えるもの
ボートレーサーからは「この場は得意だ」「苦手だ」といった声が聞かれます。
残念ながら、その節に出走するレーサーが、その場をどれくらい得意にしているかを数値化するデータ分析の腕は私にはありませんが、ボートレースの出走表には、ありがたいことに各レース場での出走成績を数値化したものが「当地成績」として記載されています。
そこで、全国勝率と当地勝率を比較して、当地勝率の方が高いレーサーを「その場に強い」とここでは定義し、そうしたレーサーが1着を取る割合（比率）が全体と比べてどうなのかを、統計学の手法のひとつである仮説検定で見てみましょう。
その場に強いレーサーの勝率が、全体との比較で「明らかに違いがある」かを、統計学がどう判断するかが、今回の検証の鍵となります。
検証に用いたデータと対象条件
仮説検定を進めるため、まずはデータを集計し、必要な値を準備しましょう。
今回の検証では、分かりやすさを考慮し、ある半年間のデータから、6艇でスタート・ゴールしたレースを対象とします。
また、当地勝率もしくは全国勝率に「0.00」が含まれているレーサーが出走しているレースを取り除いて、集計しました。
その中で、約12,000レースに出走したレーサー全員の全国勝率と当地勝率を比較し、当地勝率の方が高かったレーサーを「当地に強い」と定義して、その勝率を「調べた確率」として算出します。
この「調べた確率」と「基準の確率」に違いがあるかを、仮説検定で検証します。
全体データをどう基準にするか
ここで、検定に必要な値である「基準の確率」を確認しましょう。
今回の検証では、基準となる確率は全体の勝率にあたりますが、これは各レーサーの「当地に強いのか？」を調べるために、出走した全レーサーを基準の対象とします。
そして、そのレーサーが1着を取った割合が基準となる確率です。
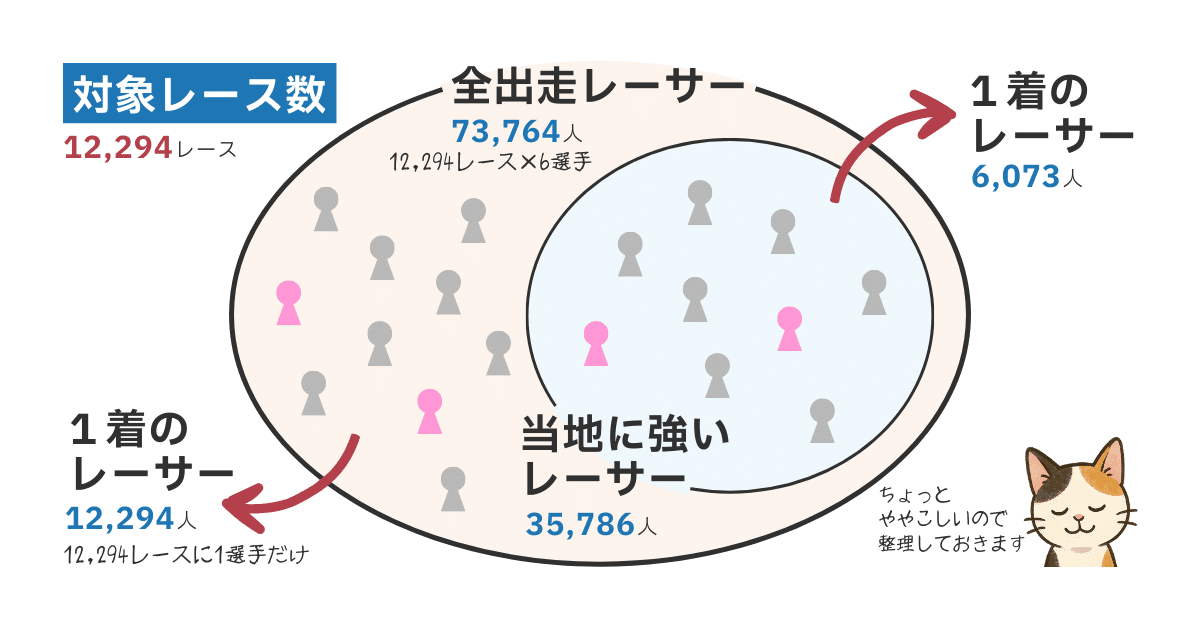
具体的な数字を挙げると、使用するデータとなる12,294レースに出走しているレーサーは73,764人（レース数 × 6選手）、そのうち1着を取ったレーサーはレース数と同じ12,294人です。
つまり、基準の確率を 12294 ÷ 73764 と計算し、16.7%とします。
当地に強いレーサーの勝率は？
一方、私たちが知りたいのは「当地に強い」レーサーが本当に強いのかどうかです。その疑問に答えるため、基準の確率と比較するのは、そのレーサーが1着を取る確率です。
そのため、約73,000人の全出走レーサーのうち、当地勝率が全国勝率を上回っていた35,786人が1着を取った確率を知る必要があり、その値は17.0%でした。
このふたつの値を見比べてみると、17.0%と16.7%ではあまり違いがありそうに感じない方もいるでしょうし、逆に「案外違いがあるな」と思った方もいるかもしれません。
このように、人によって捉え方が異なるこれらの数値を、明確な線引きをした上で違いがあるかどうかを検証し、一応の結論を出すことが、今回の目的です。
実際に、仮説検定を進めていきましょう。
仮説検定の流れを確認
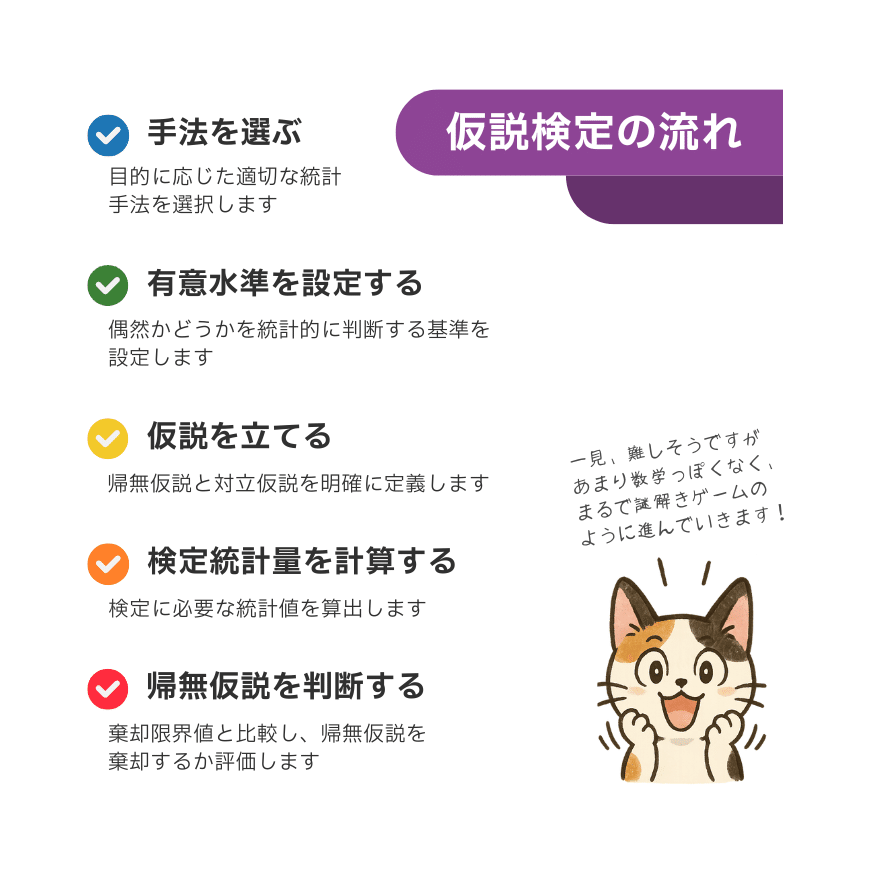
それでは、上の画像にある流れに沿って仮説検定を始めましょう。ここでは、青色と緑色のマークの項目を中心にお話しします。
まずは、数ある仮説検定の手法で、どのようなものを使用するかを考えてみましょう。
私たちが検証しようとしていることは、全体の勝率と当地に強いレーサーの勝率を比較しようとしています。さらに、それらに「違いがあるのか？」を知りたいと考えています。
これは、「全体」というひとつの群れを基準に、当地に強いレーサーの勝率（比率）がどうなのかを知りたいので、母比率の検定を採用しましょう。
さらに、「違いがある」という表現を「大きすぎる、もしくは小さすぎる」と置き換え、これを判定できるルールを使用します。
つまり、今回は「母比率の検定（両側）」を採用します。
そして、有意水準は、先ほどのような確率に対する感じ方を統一するために、あらかじめ決めておくもので、目的に応じた数値を設定します。
ここでは、過去にお話しした通り、一般的によく使われている5%という数値を、この値に設定します。
5%より少ない事柄を「偶然ではない」「稀である」とする考え方といえるでしょう。
帰無仮説と対立仮説を設定
次に、黄色の項目に進みます。
これは「仮説検定」という名前の通り、仮説を立て、その説が正しいといえるのかを結論付ける統計手法です。
ここで、実際に検証する仮説となる帰無仮説と、検証した結果を否定する際に採用する対立仮説を、あらかじめ決めておきましょう。
一般的には、私たちが知りたい事柄を対立仮説に、その逆を帰無仮説にするとされています。
今回の検証では、「全体の勝率と当地に強いレーサーの勝率に違いはあるのか？」ということなので、対立仮説は「全体の勝率と当地に強いレーサーの勝率に違いがある」とします。
そうなると、帰無仮説は「全体の勝率と当地に強いレーサーの勝率に違いはない」となり、この説が立証できるかを統計学に委ねます。
帰無仮説が否定（棄却）されるかどうかが、この検証の最大のポイントです。
基準確率・調べた確率から求める
次に、オレンジ色の項目に進みます。この検定で唯一の、具体的に数字を計算するパートになります。
検定統計量は、仮説検定で検証に必要な値で、先ほど集計したデータから計算します。
なお、検定統計量を算出するための方程式は以下になります。
これに、先ほどの「基準の確率」「調べた確率」「調べた数」を当てはめることで、検定統計量を知ることができます。
先ほど集計したデータを確認しながら、実際に方程式に値を代入して、検定統計量を計算してみましょう。
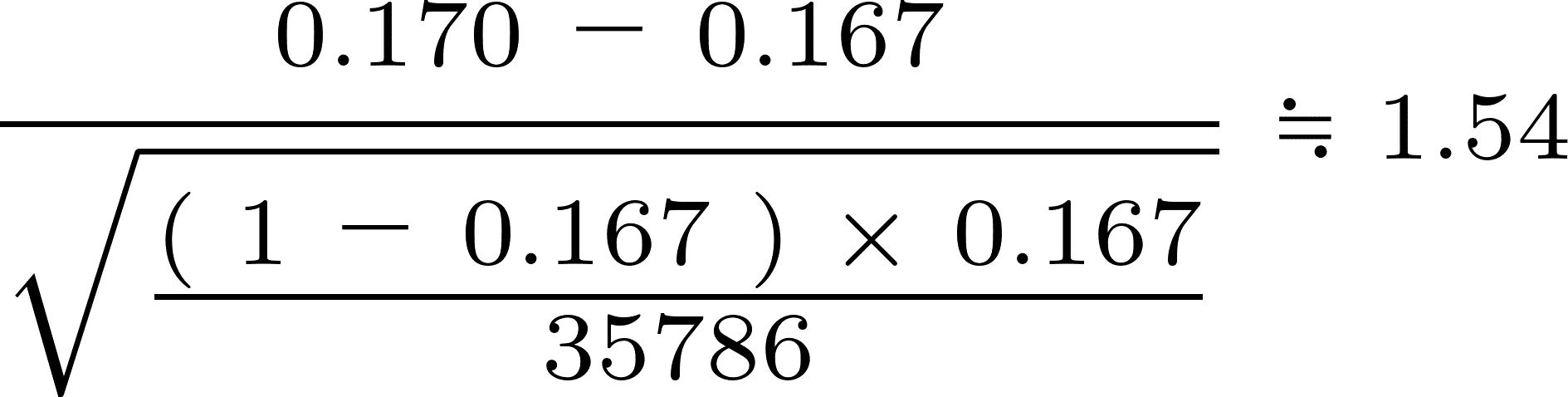
母比率の検定による最終判断
母比率の検定（両側）も、いよいよ最終段階です。
先ほど計算した検定統計量1.54を判定用のグラフに置き、統計学に最終判断をしてもらいましょう。
具体的には、下のグラフの横軸に検定統計量を配置して、その値がどの位置にあるかで、帰無仮説を採用するか、棄却して対立仮説を主張するかを判断します。
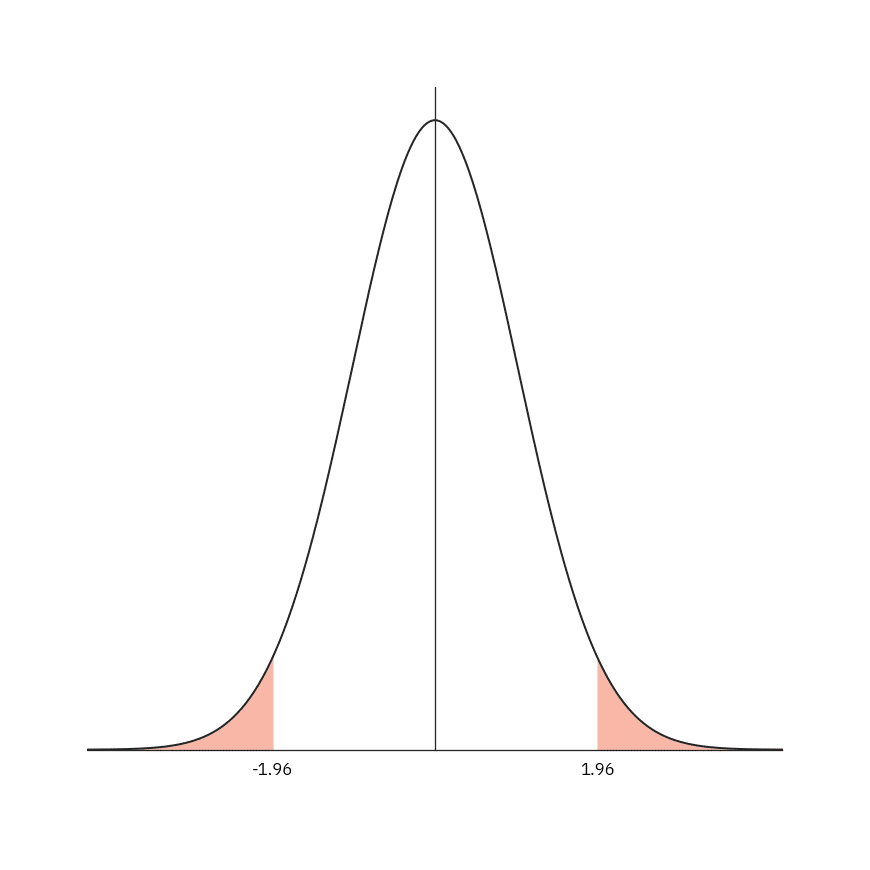
なお、グラフの白色のところに検定統計量があったときは、帰無仮説が採用され「全体の勝率と当地に強いレーサーの勝率に違いはない」と結論付けられます。
また、ピンク色の部分（棄却域）に属していた場合、帰無仮説は棄却され、対立仮説を採用します。
つまり「全体の勝率と当地に強いレーサーの勝率に違いがある」と、統計学が判断したことになります。
さて、今回の検証を統計学はどうジャッジしたのでしょうか──
「当地に強い」は勝率上昇の要因か？
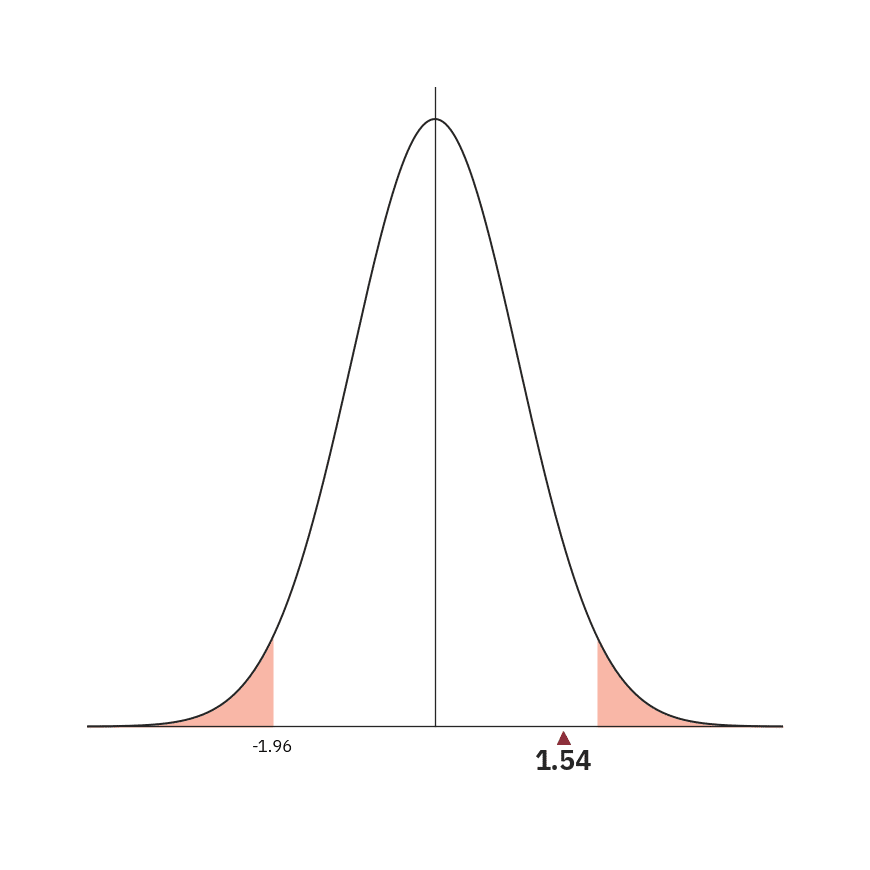
上のグラフを見ると、検定統計量の1.54はグラフの白色の部分にあります。
これは、帰無仮説の採用を意味し「全体の勝率16.7%と当地に強いレーサーの勝率17.0%には明確な違いはない」と判断されたことになります。
これを噛み砕いて、ここでは「全国勝率より当地勝率の方が高いレーサーが、特別多くの1着を取るわけではない」としておきましょう。
「当地に強いレーサー」は、その場の勝率が高い分、節間は大活躍だろうと考えていましたが、今回の集計期間や条件で検証する限りでは、的中率上昇の重要ファクターではないという結果でした。
見方によっては必須ファクターにも？
かといって、出走表の当地勝率のデータが、ボートレース予想において不必要かというと、それも少し強引ではないでしょうか。
異なる切り口でデータ分析をすれば、舟券戦略に使えるファクターになる可能性もありますし、集計データを増やせば違った結果になるかもしれません。
皆さんは「当地勝率」をどう料理して、ボートレースに活かしますか？ぜひ、ご意見を聞かせてください。
次回は「特に当地成績が重要だ」といわれているあの場の話題を中心に、もう少し掘り下げてみようと考えています。